F-14 TDI: Aircraft Stabilized Mode

The previous article introduced the Ground Stabilized mode, a “Bird’s eye” view of the area. This article is about the mode that is both the more often utilized and the less intuitive to understand: Aircraft Stabilized.

---

Quoting the manual:

Velocity vector emanating from center dot of tracks when velocity vector display is selected.

Vector direction represents track heading and length represents track speed so that the max indicated speed (1 800 knots) is 1.5 inches on the TID.

In TID ground stabilized mode the vector direction represents track true heading and the vector length represents track ground speed.

In TID aircraft stabilized and attack modes the vector direction represents track relative heading (to own aircraft) and the vector length represents track speed relative to own aircraft.

The question is: what does relative heading mean?.

Not really intuitive

If you are familiar with modern fixed wing aircraft this is something you know already. If you are not (like myself), the representation of the contacts on the TID in Aircraft Stabilized mode may appear a bit confusing.
Consider the following example:

This looks like a simple scenario: a target is going South, the other South-East, right? Not at all. This is how they look like in the mission editor:

One of the targets is heading South-East (not the one we were thinking!) and the other is going.. North-East! This scenario raises the question: how is the VV (Velocity Vector) determined? The answer is not difficult at all, but let’s first introduce the Vectors.

Vectors

Vectors are one of the very first topics studied in high schools in Physics so I won’t spend more than two words on them. Nevertheless, it is important to understand how they work.
The specific family of vectors I’m referring to is the Euclidean. We are going to use them to represent the motion of our F-14 and other contacts. In very simple words: the length of the vector (“norm“) corresponds to the speed and the angle between the origin and the terminal point of the vector (direction) represents the heading.
The interesting thing about Vectors is that they can simply added and subtracted by means of geometry.

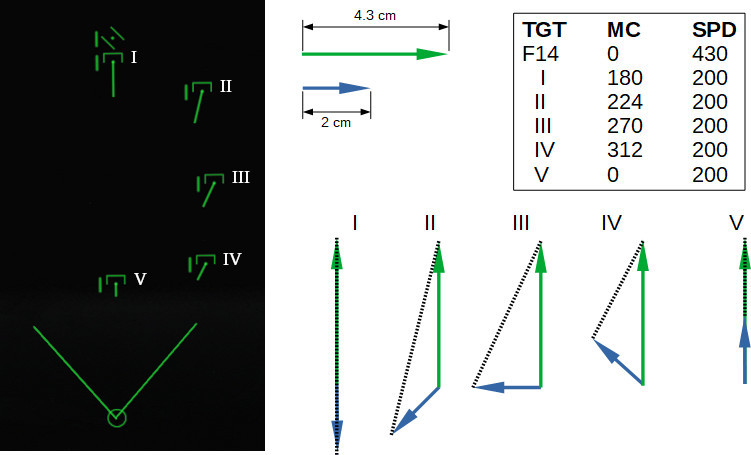
Gathering data

By means of Tacview, I collected Speed and Heading of each aircraft in the scenario presented above:

NOTE: in order to make the example more interesting, I placed the aircraft randomly. That may create a couple issues due to the now needed approximation.
These are the vectors of each aircraft. The graphical representation is an approximation but still proportional to the values:

As I mentioned before, vectors can be subtracted geometrically. Let’s do that and compare the result with the TID AS view:

Impressively similar, right?

Example II: Ground Stab scenario

Another example. This is the same test I used in the previous article about the TDI in Ground Stab mode:

The result is quite easy to determine because our F-14 is HDG due North.

Example III: Ground Stab scenario + HDG Offset

What if the heading of our F-14 is not due North? This is the result of asking Iceman to turn 30° to the right. The scenario is the same seen in the Example II.
In primis, since our HDG is not zero, we have to recalculate the headings (“RHDG”) of the contacts by subtracting our HDG. Remember that AS mode is relative to our aircraft.
The result is again quite clear:

Example IV: from GS’ PvP Server livestream

Let’s look at another example. This is from my stream on Growling Sidewinder’s PvP server:

This is both Tacview and TID from the moments before the second FOX3. This situation is more complex than the previous. Not only the heading must be recalculated (round brackets); moreover, the Vector displayed on the TID is now different because it has been replaced by the Launch Zone Vector.

Example V: Faster contacts

Until now, every contact was either slower or had similar speed. What if the contacts are faster? Let’s find out.
This is the same Ground Stabilized scenario seen above, but I “inverted” the speeds: the F-14 is now flying at 200kts whereas every other contact is flying at 430kts.

The resolution is not different from the previous. Nevertheless we see for the first time a VV pointing “up”.
You may have noticed that one of the target comes only from the DL and not the AWG-9. The reason is simple: zero doppler filter.

Example VI: BVR Practice

The last example is from a recent BVR practice. Scenario is 2x F/A-18 vs 1x F-14B.
Understanding how the Velocity Vectors is displayed on the TID, allows you to establish where the contacts are heading and estimate their speed at a glance.

The VV of the left target coming via DL is still visible under the LZ indicator.

Model and Observations

To better understand how the VV works and make some immediate “rules of thumb”, I prepared a series of tests, covering different angles and ΔSpeeds:

The F-14 (blue) is always travelling at 400kts. The Target (green) flies between 100kts to 900kts. I considered angles between 30° and 150°.

I skipped the case of having both the same heading and opposite heading. In both scenarios the vector of the F-14 and the vector of the target overlap. The length is determined by the difference of the norms, the same as the direction.

I then plotted the resulting vectors on a circle (semicircle actually, since it’s symmetric) and marked where the tip of the vector was landing.
As you may have guessed already, a discriminating factor is the speed of our aircraft. Looking at the previously posted set of vectors, it’s clear how they change as the speed of the contact is higher than the speed of the F-14 and the semicircles shown below clearly prove that pattern.

NOTE: The radius of the internal semicircumference is as long as the norm of the vector of the F-14. The radius of the external semicircumference instead is not relevant.

At 30° or less, the VV is very short and points upwards as the ΔV increases.
At 45°, the angle is never acute if V_TGT < V_F14. The VV moves to the higher part of the contact symbol only when the target is faster but it doesn’t reach angles as acute as in the 30° scenario.
At 60°, the VV tends to be between 135° and 90° most of the times.
The 90° scenario is very interesting. You can tell immediately that the angle, as long as the speeds are comparable, is close to 135°. Moreover, the projection of VV_TGT on the Vector of VV_F14, is exactly as long as the VV of the F-14 itself. If you see this (MLC off or via DL), the target is perfectly notching.
From 105° to 150° the VV is never acute and the angle is almost always greater than 135°. The more the VV gets longer and closer to be perpendicular to the bottom of the TID, the higher are the chances that the target is coming head-on.

Wrapping it up

These are general observations, they do not apply to extreme scenarios (such as the F-14 flying at 200kts and a target flying at Mach 2) but they should help understand the patterns of the VV and what it means.

• If the VV is longer than the VV_F14, then the target is faster than the F14, no matter the direction.
• The shortest the VV, the closer the target is to COLD aspect.
• If the VV points upward, the target is definitely faster than the F14. The more acute the angle is, the more the aspect of the target tends to COLD.
• If the VV is longer than the VV_F14 and the angle > ~135°, then the target HDG is between 90° and 180° (BEAMING and HOT).
• A ~45° angle means that the target is travelling at a fairly similar speed and notching.
• As the HDG_TGT tends to 90°, the length of the projection of its VV is equal to the VV of the F14.

There are probably more valuable observations to make. If I think about more (or you suggest some others), I will add them to the list.

Eyeballing the length of the VV

We noticed how the length of the VV can help to determine more accurately the speed and the aspect of the target. The problem is, how do know how long is the vector?
To answer this question, I create a simple scenario: an F-14 is coming head-on at 200kts. The speed of our F-14 is 200kts as well. I then printscreened the result, created a sketch of the target icon in Libreoffice Draw, rescaled it to make sure that the VV was exactly 4cm (therefore 1mm = 10kts) and measured the other dimensions.
This is the result:

The flat, top, part of the “T” is 3.52cm. Therefore it corresponds to approximately 350kts. The vertical, shorter, part of the “T” is 170kts. As expected, the stem of the “T” is 40mm, ergo 400kts.

---

Well, that’s pretty much it. I hope you enjoyed!

The point of this article is not providing means of obtaining a precise measurement, whereas it is to give some ideas, some starting points, in order to ease the understanding of how this means of representing information on the TID works.
At some point, with some practice, processing and understanding the TID will become a simple and automatic routine.

Thanks to 132nd.Looney for reviewing the article and for the inputs in the discussion about the TID in Aircraft Stabilized mode.